AVL树的全称是平衡搜索二叉树，本质上也是一个二叉搜索树（BST），满足BST树的所有性质。

AVL简介

在BST中搜索一个结点的平均时间复杂度是O(lgn)，最坏情况会出现O(n)，即出现连续的左/右子树：

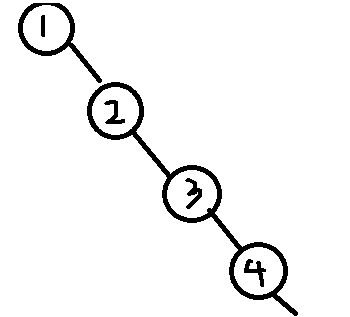
image-20200722110541352

这种情况其实就已经是链式存储，无法将树的优势体现出来。为了避免这种情况，我们就要保证这个树随时都是平衡的。当然要求不能那么严格，不需要保证它完全平衡（每个节点的左右子树高度差的绝对值都为0），AVL树就要求的是只要每个节点的左右子树高度差的绝对值不超过1，就可以称作平衡。

AVL自旋

平衡因子(BF)：每个节点的左右子树的高度差的绝对值

在AVL树中，插入一个节点之后都会判断是否打破了这个平衡。如果打破了，就需要对树进行调整，让它仍然满足平衡的定义，并且不改变中序遍历的正确性。这步操作就叫做旋转。即，是否需要旋转以及具体的旋转实现都要包含在插入函数里。

根据插入的位置不同，旋转的类型也分为4种：LL，LR，RL，RR：

  • 左左LL：插入点位于x的左孩子的左子树中，右旋。
  • 左右LR：插入点位于x的左孩子的右子树中，较低的先左旋，转换为LL问题，再右旋。
  • 右左RL：插入点位于x的右孩子的左子树中，较低的先右旋，转化为RR问题。再左旋。
  • 右右RR：插入点威武x的右孩子的右子树中，左旋。

自旋详解

AVL树定义以及前置函数定义：

typedef struct AVLTree
{
    int height;                //当前节点的高度。
    int data;
    struct AVLTree* lchild;
    struct AVLTree* rchild;
}Tree,*pTree;

int GetHeight(pTree tree)            //获取当前节点的高度。
{
    if(tree == nullptr) return 0;
    return tree->height;
}
 
bool IsBalanced(pTree tree)            //判断是否平衡。
{
    int BF = GetHeight(tree->lchild) - GetHeight(tree->rchild);
    return abs(BF) < 2;
}

左左LL

导致失衡的节点node(1)是节点node(3)的左子树的左孩子，即为LL情况。

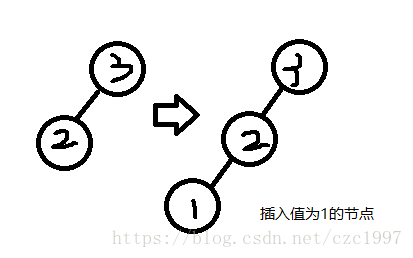
image-20200722111715724

算法步骤：

  1. 对于节点node(3)，先取它的左孩子node(2)作为临时节点temp；
  2. 将temp的右孩子作为node的左孩子；
  3. 再将node作为temp的右孩子；
  4. 更新height
  5. node = temp。此时，temp就成为了原来node一样的存在。
pTree Rotate_LL(pTree tree)
{
    pTree temp = tree->lchild;
    tree->lchild = temp->rchild;
    temp->rchild = tree;
 
    //更新高度,先更新node再更新temp。
    tree->height = max(GetHeight(tree->lchild),GetHeight(tree->rchild))+1;
    temp->height = max(GetHeight(temp->lchild),GetHeight(temp->rchild))+1;
 
    return temp;
}

调整结果：

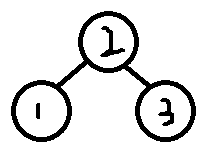
image-20200722111910017

右右RR

RR型由于和LL型是对称的，所以只需要将LL中的所有左右互换就可以了。

pTree Rotate_RR(pTree tree)
{
    pTree temp = tree->rchild;
    tree->rchild = temp->lchild;
    temp->lchild = tree;
 
    //更新高度,先更新node再更新temp。
    tree->height = max(GetHeight(tree->lchild),GetHeight(tree->rchild))+1;
    temp->height = max(GetHeight(temp->lchild),GetHeight(temp->rchild))+1;
 
    return temp;
}

左右LR

引起失衡的是node节点的左子树的右孩子。

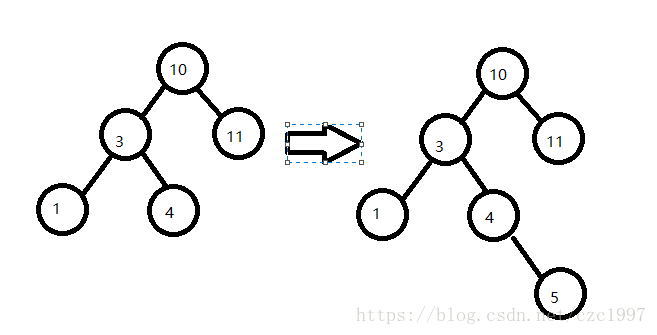
image-20200722113201966

在节点值为4的节点插入5，是4的右孩子。此时已经失衡。即为LR问题。

算法步骤：

  1. 先获取node（值为10的节点）的左孩子节点，记为temp。

  2. 对temp进行RR。

  3. 对node进行LL。

pTree Rotate_LR(pTree tree)
{
    pTree temp = tree->lchild;
    tree->lchild = Rotate_RR(temp);
    return Rotate_LL(tree);
}

右左RL

RL型由于和LR型是对称的，所以只需要将LR中的所有左右互换就可以了。

pTree Rotate_RL(pTree tree)
{
    pTree temp = tree->rchild;
    tree->rchild = Rotate_LL(temp);
    return Rotate_RR(tree);
}

总体代码

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
typedef struct AVLNode *position;
typedef position AVLTree;
struct AVLNode{
	int data;
	AVLTree left;
	AVLTree right;
	int h;
};
int GetHight(AVLTree A){
	if(A == NULL)	return -1;
	return A->h;
}
//左单旋
AVLTree SLR(AVLTree A){
	AVLTree B = A->left;
	A->left = B->right;
	B->right = A;
	A->h = max(GetHight(A->left),GetHight(A->right))+1;
	B->h = max(GetHight(B->left),GetHight(B->right))+1;
	return B;
} 
//右单旋
AVLTree SRR(AVLTree A){
	AVLTree B = A->right;
	A-> right = B->left;
	B->left = A;
	A->h = max(GetHight(A->left),GetHight(A->right))+1;
	B->h = max(GetHight(B->left),GetHight(B->right))+1;
	return B;
}
//左右双旋
AVLTree DLRR(AVLTree A){
	AVLTree B = A->left;
	A->left = SRR(B);
	return SLR(A);
}
//右左双旋 
AVLTree DRLR(AVLTree A){
	AVLTree B = A->right;
	A->right = SLR(B);
	return SRR(A);
}
AVLTree Insert(AVLTree T,int x){
	if(T == NULL){
		T = new AVLNode();
		T->data = x;
		T->left = NULL;
		T->right = NULL;
		T->h = 0;
	}else if(x < T->data){
		T->left = Insert(T->left,x);
		if(GetHight(T->left) - GetHight(T->right) == 2)
			if(x < T->left->data)	T = SLR(T);
			else T = DLRR(T);
	}else if(x > T->data){
		T->right = Insert(T->right,x);
		if(GetHight(T->left)-GetHight(T->right) == -2)
			if(x > T->right->data)	T = SRR(T);
			else	T = DRLR(T);
	}
	T->h = max(GetHight(T->left),GetHight(T->right))+1;
	return T;
}

参考文章

数据结构：AVL树的平衡调整——LL，LR，RL，RR

AVL树的调整（笔记）